隐私保护技术方案中密码学算法的安全性分析与应用思考

imToken钱包致力于为全球用户提供简单、高效、安全的区块链资产管理解决方法。

密码学算法的不对称性亮点

密码学中的非对称特性非常奇妙，尤其在隐私保护方面表现得尤为突出。相同的隐私信息，通过不同的计算途径获取，其难度差异显著。举个例子，面对一个复杂的谜题，解答它和验证答案是否正确，其难度可谓天壤之别。这种不对称性正是密码学算法安全的核心，也激发了我们对其浓厚的兴趣！

计算困难性理论表现

隐私保护领域，计算难度的不均衡性十分明显。采用不同的计算手段处理隐私信息，即便获取的信息一致，所需难度却相差悬殊。这就像攀登山路，一条路平坦，另一条则布满荆棘。较易的计算途径适用于授权数据访问，而难度较大的计算则能阻止未授权数据的泄露，从而有效维护信息安全。

NP问题的奇妙之处

NP问题性质独特，确定性图灵机能在多项式时间内检验答案是否正确，但未必能计算出答案。以解复杂数学题为例，验证答案是否正确可能相对简单，但求出答案却仿佛攀登天梯。这种验证与计算的难度差异，使得我们可以构建出密码学算法所需的计算难度不均衡性，从而为密码学的发展开辟了新的路径。

NP与P问题的关联挑战

将NP问题转变为P问题是一项重大挑战。若能发现一种多项式时间内的有效算法实现这一转变，那么密码学的计算难度不均衡性或许会被突破。至于NP完全问题这一核心难点，若能攻克其中之一，那么其他NP问题也将有可能找到相应的有效解决方案。现代计算机在短时间内尚无法解决这些问题，因此以NP完全问题为基础的密码学算法相对较为安全。

密码学算法示例剖析

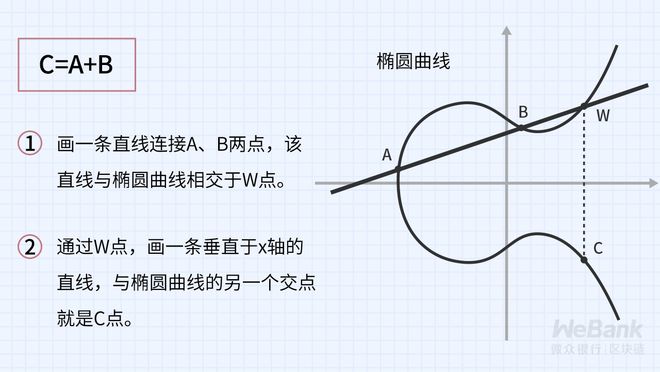
日常所用的密码学方法，众多都与那个理论紧密相连。比如，非对称密码学方法，它有一个著名的“迷宫构建图”，即那三个计算难题。其中，大整数分解问题经常被运用，比如RSA系列方法，因为目前还没有更有效的分解方法，所以将密码学方案的安全性归结为大数分解的难题，以此来确保安全。

椭圆曲线密码学算法优势

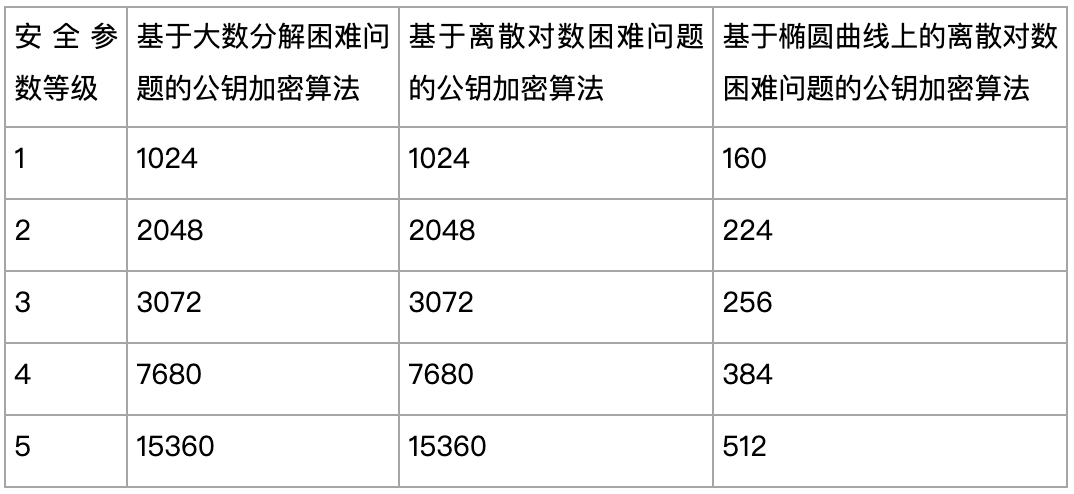
椭圆曲线密码学算法在密码应用中占据主流地位。隐私数据可以转换成椭圆曲线上的坐标点。不同的密码学算法基于不同的难题来构建，而这些难题又各自有着不同的安全前提。企业在选择技术方案时，弄清楚这些安全前提至关重要，否则就如同不明水情就下水游泳，很容易遇到麻烦。

安全参数的重要影响

安全参数对密码学算法的运作至关重要。若未明确安全参数，仅凭算法去评判其安全性，就如同空谈兵法，毫无实际意义。若安全参数数值偏低，密钥长度不足，即便是再优秀的算法也可能存在安全隐患。密码学算法并无绝对的最强版本，它们只在特定安全假设下具备足够的强度。盲目比较基于不同难题的算法强弱，实际上并无实际意义。

企业算法选型的关键因素

企业在选择密码学算法时，计算难度和安全要素是至关重要的考量。只有深刻理解计算难度，才能挑选出满足特定需求的算法；只有熟练掌握安全参数，算法才能达到最佳效果。这就像选用工具，只有清楚工具的适用环境和操作方法，才能得心应手。

密码学协议的重要作用

算法本身存在计算上的挑战，而要构建一个全面的隐私保护措施，还需要密码学协议的支持。这些协议能够将不同的密码学算法融合，打造出更为坚固的保护网络。就好比建造房屋，算法如同砖块，而协议则是将砖块粘合在一起的水泥，增强了整个结构的稳定性。

在使用电子产品时，我们是否思考过支撑我们信息安全的是怎样的密码学原理？不妨点个赞，把这篇文章转发出去，让我们共同揭开密码学的神秘面纱！

imToken钱包全球领先的区块链钱包,为千万用户提供可信赖的服务。